Selection Example - Ball Screw Mechanism | Selection Procedures and Calculation Formulas

For AC motors

(1) Specifications and Operation Conditions of the Drive Mechanism

This is a selection example when using an electromagnetic brake motor in the vertical operation of a table using a ball screw.
A motor must be selected that meets the following required specifications.

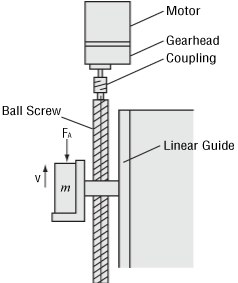
Total Mass of Table and Load: m = 45 [kg]

Travel Speed of Table: V = 15 ± 2 [mm/s]

External Force: F_A = 0 [N]

Ball Screw Inclination Angle: θ = 90 [˚]

Overall Length of Ball Screw: L_B = 800 [mm]

Shaft Diameter of Ball Screw: D_B = 20 [mm]

Ball Screw Lead: P_B = 5 [mm]

Travel Distance per Ball Screw Revolution: A = 5 [mm]

Ball Screw Efficiency: η = 0.9

Ball Screw Material: Iron (density ρ = 7.9 × 10³ [kg/m3])

Internal Friction Coefficient of Preload Nut: μ₀ = 0.3

Friction Coefficient of Sliding Surface: μ = 0.05

Motor Power Supply: Single-Phase 100 VAC 60 Hz

Operating Time: Intermittent operation 5 hours per day

Load Holding Required While Stopping for Repeated Start/Stop

(2) Determine the Gear Ratio of Gearhead

\(\begin{align} \text{Gearhead Output Shaft Speed}\ N_G=\frac{V \cdot 60}{A} &= \frac{(15 \pm 2) \times 60}{5}\\[ 5pt] &= 180 \pm 24\ [ \mathrm{r/min}]\end{align}\)

Since the rated speed for the electromagnetic brake motor (4-pole) at 60 Hz is 1450-1550 [r/min], select a gearhead gear ratio within this range.

\(\begin{align} \text{Gearhead Gear Ratio}\ i=\frac{1450\text{～}1550}{N_G} &= \frac{1450\text{～}1550}{180 \pm 24} =7.1\text{～}9.9 \end{align}\)

Select a gear ratio of i = 9.

(3) Calculate the Required Torque T_M [N·m]

\(\begin{align} \text { Force of moving direction }F & = F_A+m \cdot g\ (\sin \theta+\mu \cdot \cos \theta)\\[ 5pt ] & = 0 + 45 \times \ 9.807(\sin 90^{\circ}+\ 0.05 \cos 90^{\circ})\\[ 5pt ] & = 441\ [\mathrm{N}]\end{align}\)

\(\begin{align} \text { Ball screw preload }F_0 = \frac{F}{3} = 147\ [\mathrm{N}]\end{align}\)

\(\begin{align} \text { Load Torque } {T'}_L & =\frac{{F} \cdot {P_B}}{2 \pi \cdot \eta} + \frac{ \mu_0 \cdot F_0 \cdot P_B}{2 \pi} \\[ 5pt ] & =\frac{441 \times 5 \times 10^{-3}}{2 \pi \times 0.9} + \frac{0.3 \times 147 \times 5 \times 10^{-3}}{2 \pi} \\[ 5pt ] & =0.426\ [\mathrm{N} \cdot \mathrm{m}] \end{align}\)

Consider the safety factor Sf = 2.

\(T_L = {T'}_L \cdot S_f = 0.426 \times 2 = 0.86 \ [\mathrm{N}\cdot \mathrm{m}]\)

Select an electromagnetic brake motor and gearhead satisfying the permissible torque of gearhead based on the calculation results (gear ratio i = 9, load torque T_L = 0.86 [N·m]) obtained so far.
Here, 4RK25GN-AW2MJ and 4GN9K are tentatively selected as the motor and gearhead respectively, by referring to the specifications.
Convert this load torque to a value on the motor output shaft to obtain the required torque T_M.

\(\begin{align}T_M = \frac{T_L}{i \cdot \eta _G} = \frac{0.86}{9 \times 0.81} = 0.118 \ [\mathrm{N}\cdot \mathrm{m}] = 118\ [ \mathrm{m} \mathrm{N}\cdot \mathrm{m}] \end{align}\)

(Gearhead 4GN9K transmission efficiency η_G = 0.81)

The starting torque of the 4RK25GN-AW2MJ motor selected earlier is 140 [mN·m]. Since this is greater than the required torque of 118 [mN·m], this motor can start the mechanism.
Also confirm whether the electromagnetic brake can hold the gravitational load exerted during stopping.
Here, the load is assumed to be equivalent to the load torque calculated earlier.
Torque T'_M

required for load holding on the motor output shaft

\(\begin{align}{T'}_M = \frac{T_L}{i} = \frac{0.86}{9} = 0.0956 \ [\mathrm{N}\cdot \mathrm{m}] = 95.6 \ [ \mathrm{m} \mathrm{N}\cdot \mathrm{m}] \end{align}\)

The static friction torque of the electromagnetic brake for the previously selected 4RK25GN-AW2MJ is 100 [mN·m], which meets the required torque of 95.6 [mN·m] for load holding.

(4) Check the Load Inertia J [kg·m²]

Inertia of Ball Screw

\(\begin{align} {J_B} & = \frac{\pi}{32}\cdot \rho\cdot{L_B}\cdot{{D_B}^4}\\[ 5pt ] & = \frac{\pi}{32}\times\ 7.9 \times 10^3\ \times 800 \times 10^{-3}\times {\left(20\times 10^{-3} \right)}^4\\[ 5pt ] & = 0.993 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}] \end{align}\)

Inertia of Table and Load

\(\begin{align} {J_m} & = \mathrm{m}\ \left(\frac{A}{2\pi}\right)^2\\[ 5pt ] & = 45 \left(\frac{5 \times 10^{-3}}{2\pi}\right)^2\\[ 5pt ] & = 0.286 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}] \end{align}\)

Calculate the load inertia for the gearhead output shaft J.

\(\begin{align} J &= J_B + J_m = 0.993 + 0.286\\ &= 1.28 \times {10}^{-4}\ [\mathrm{kg} \cdot \mathrm{m^2}] \end{align}\)

Here, permissible load inertia J_G for gearhead 4GN9K with a gear ratio 9 is given by the following formula.

\(\begin{align} J_G &= 0.31 \times {10}^{-4} \times 9^2\\ &= 25.1 \times {10}^{-4}\ [\mathrm{kg} \cdot \mathrm{m}^2] \end{align}\)

Therefore, J < J_G, the load inertia is less than the permissible value and there is no problem. There is margin for the torque, so the travel speed is checked with the rotation speed under no load (approximately 1750 r/min).

\(\begin{align} V &= \frac{N_M \cdot P_B}{60 \cdot i} = \frac{1750 \times 5}{60 \times 9} = 16.2\ [\mathrm{mm} / \mathrm{s}] \quad\quad N_M: \text{Motor speed} \end{align}\)

This confirms that the motor meets the specifications.
Based on the above, 4RK25GN-AW2MJ and 4GN9K are selected as the motor and gearhead, respectively.

For αSTEP/Stepper motors

(1) Specifications and Operation Conditions of the Drive Mechanism

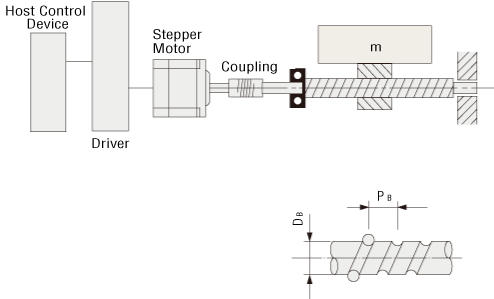
Total Mass of Table and Load: m = 40 [kg]

Friction Coefficient of Sliding Surface: μ = 0.05

Ball Screw Efficiency: η = 0.9

Internal Friction Coefficient of Preload Nut: μ0 = 0.3

Shaft Diameter of Ball Screw: D_B = 15 [mm]

Overall Length of Ball Screw: L_B = 600 [mm]

Ball Screw Material: Iron (density ρ = 7.9 × 10³ [kg/m³])

Ball Screw Lead: P_B = 15 [mm]

Required Resolution (Feed per pulse): Δl = 0.03 [mm/step]

Feed Amount: l = 180 [mm]

Positioning Time: t₀ = Within 0.8 seconds

Inclination Angle: θ = 0 [˚]

(2) Calculate the Required Resolution θ_S

\(\begin{align} \theta_S &= \frac{360^\circ \cdot \Delta l}{P_B}\\[ 5pt ] &= \frac{360^\circ \times 0.03}{15}= 0.72^\circ \end{align}\)

αSTEP AZ Series can be used.
Changing or setting the resolution is possible.
The factory setting resolution can be changed from 0.36˚/pulse → 0.72˚/pulse.

(3) Determine an Operating Pattern

Refer to formula

① Calculate the number of operating pulses A [Pulse]

\(\begin{align} A &= \frac{l}{P_B} \cdot\frac{360^\circ}{\theta_S}\\[ 5pt ] &= \frac{180}{15} \times \frac{360^\circ}{0.72^\circ}= 6000\ [\text{Pulse}] \end{align}\)

② Determine the acceleration (deceleration) time t₁ [s]

An acceleration (deceleration) time of 25 % of the positioning time is appropriate.

\(\begin{align} t_1= 0.8 \times 0.25 = 0.2 \ [\mathrm{s}] \end{align}\)

③ Calculate the operating pulse speed f₂ [Hz]

\(\begin{align} f_2 &= \frac{A - f_1 \cdot t_1}{t_0 - t_1} \\[ 5pt ] &= \frac{6000 - 0}{0.8 - 0.2} = 10000\ [\text{Hz}] \end{align}\)

③ Calculate the operating pulse speed f2 [Hz]

④ Calculate the operating speed N_M [r/min]

\(\begin{align} N_M &= \frac{\theta_S}{360^\circ} f_2 \cdot 60\\[ 5pt ] &= \frac{0.72^\circ}{360^\circ}\times 10000 \times 60\\[ 5pt ] &= 1200\ [\text{r/min}] \end{align}\)

(4) Calculate the Required Torque T_M [N·m]

Refer to formula

① Calculate the load torque T_L [N·m]

\(\begin{align}\text { Force of moving direction }F & = F_A+m \cdot g\ (\sin \theta+\mu \cos \theta)\\[ 5pt ] & = 0 + 40 \times \ 9.807(\sin 0^{\circ}+\ 0.05 \cos 0^{\circ})\\[ 5pt ] & = 19.6\ [\mathrm{N}]\end{align}\)

\(\begin{align}\text { Preload }F_0 = \frac{F}{3} = \frac{19.6}{3}=6.53\ [\mathrm{N}]\end{align}\)

\(\begin{align}\text { Load Torque } {T_L} & =\frac{{F} \cdot {P_B}}{2 \pi \cdot \eta} + \frac{ \mu_0 \cdot F_0 \cdot P_B}{2 \pi} \\[ 5pt ] & =\frac{19.6 \times 15 \times 10^{-3}}{2 \pi \times 0.9} + \frac{0.3 \times 6.53 \times 15 \times 10^{-3}}{2 \pi} \\[ 5pt ] & =0.0567\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

② Calculate the acceleration torque T_a [N·m]

②-1 Calculate the load inertia J_L [kg·m²] (Refer to formula)

Inertia of Ball Screw

\(\begin{align} {J_B} & = \frac{\pi}{32}\cdot \rho\cdot{L_B}\cdot{{D_B}^4}\\[ 5pt ] & = \frac{\pi}{32}\times\ 7.9 \times 10^3\ \times 600 \times 10^{-3}\times {\left(15\times 10^{-3} \right)}^4\\[ 5pt ] & = 0.236 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}] \end{align}\)

Inertia of Table and Load

\(\begin{align}{J_r} & = \mathrm{m}\ \left(\frac{P_B}{2\pi}\right)^2\\[ 5pt ] & = 40 \left(\frac{15 \times 10^{-3}}{2\pi}\right)^2\\[ 5pt ] & = 2.28 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}] \end{align}\)

Load inertia

\(\begin{align}J_L &=J_B + J_r\\ &= 0.236 \times10^{-4} + 2.28 \times 10^{-4}\\ & = 2.52 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}] \end{align}\)

②-2 Calculate the acceleration torque T_a [N·m]

\(\begin{align}T_a & =\frac{(J_0 + J_L)}{9.55} \cdot \frac{N_M}{t_1} \\[ 5pt ] & =\frac{(J_0 + 2.52 \times 10^{-4})}{9.55} \times \frac{1200}{0.2} \\[ 5pt ] & =628\ J_0 + 0.158\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

The formula for calculating acceleration torque with pulse speed is shown below. Calculation results are the same.

\(\begin{align}T_a & =(J_0 + J_L) \cdot \frac{\pi \cdot \theta_S}{180^\circ} \cdot \frac{f_2 - f_1}{t_1} \\[ 5pt ] & =(J_0 + 2.52 \times 10^{-4})\times \frac{\pi \cdot 0.72^\circ}{180^\circ}\times \frac{10000-0}{0.2} \\[ 5pt ] & =628\ J_0 + 0.158\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

③ Calculate the required torque T_M [N·m]

Safety factor S_f = 2.

\(\begin{align}T_M & =(T_L + T_a)S_f\\[ 5pt ] & =\{0.0567 + (628\ J_0 + 0.158) \} \times 2\\[ 5pt ] & =1256\ J_0 + 0.429\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

(5) Select a Motor

① Tentative Motor Selection

Product Name	Rotor Inertia [kg·m²]	Required Torque [N·m]
AZM66AC	370 x 10^-7	0.48

② Determine the Motor From the Speed - Torque Characteristics

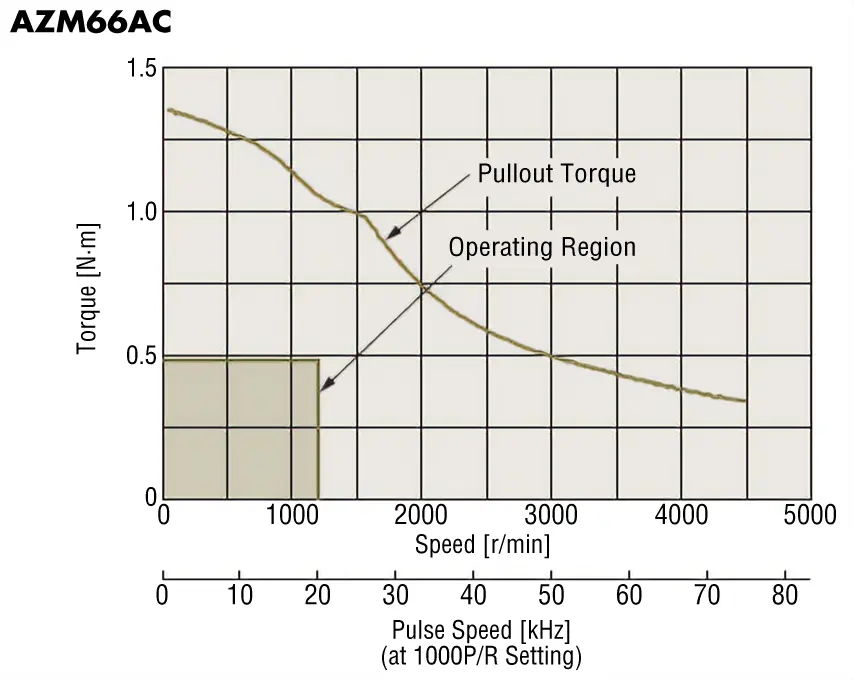
Since the duty region of the motor (operating speed and required torque) falls within the pullout torque of the speed - torque characteristics, the motor can be used.

(6) Check the Inertia Ratio

Refer to formulas and reference values

\(\begin{align}\frac{J_L}{J_0} =\frac{2.52 \times 10^{-4}}{370 \times 10^{-7}}\fallingdotseq 6.8\end{align}\)

Since the inertia ratio of

AZM66AC is 30 or less, if the calculated inertia ratio is 6.8, then operation of that motor is possible.

For Servo Motors

(1) Specifications and Operation Conditions of the Drive Mechanism

The following figure is an example of how to select a servo motor to drive a single axis table:

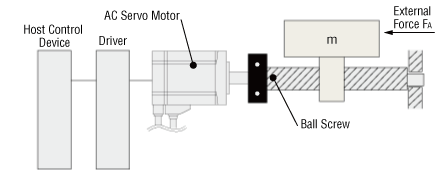
Maximum Speed of Table: V_L = 0.2 [m/s]

Resolution: Δl = 0.02 [mm]

Motor Power Supply: Single-Phase 100 VAC

Total Mass of Table and Load: m = 100 [kg]

External Force: F_A = 29.4 [N]

Friction Coefficient of Sliding Surface: μ = 0.04

Ball Screw Efficiency: η = 0.9

Internal Friction Coefficient of Preload Nut: μ₀ = 0.3

Shaft Diameter of Ball Screw: D_B = 25[mm]

Overall Length of Ball Screw: L_B = 1000 [mm]

Ball Screw Lead: P_B = 10 [mm]

Ball Screw Material: Iron (density ρ = 7.9 × 10³ [kg/m3])

Operating Cycle: Operation for 2.1 seconds/stopped for 0.4 seconds (repeated)

Acceleration/Deceleration Time: t₁ = t3 = 0.1 [s]

(2) Calculate the Required Resolution θ

Calculate the motor resolution from the resolution required for the table drive.

\(\begin{align}\theta =\frac{360^\circ \cdot \Delta l}{P_B}= \frac{360^\circ \times 0.02}{10}=0.72^\circ\end{align}\)

The resolution of the NX Series, θ_M = 0.36˚/pulse, satisfies this requirement.

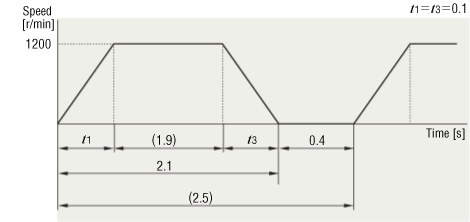
(3) Determine an Operating Pattern

Calculate the motor rotation speed (N_M) using the formula below.

\(\begin{align}N_M =\frac{60 \cdot V_L}{P_B}= \frac{60 \times 0.2}{10 \times 10^{-3}}=1200\ [\mathrm{r/min}]\end{align}\)

Determine the speed pattern using N_M, the operating cycle and the acceleration/deceleration time.

(4) Calculate the Load Torque T_L [N·m]

Operation Direction Load

\(\begin{align}F & = F_A+m \cdot g\ (\sin \theta+\mu \cdot \cos \theta)\\[ 5pt ] & = 29.4 + 100 \times \ 9.807 \ (\sin 0^{\circ}+\ 0.04 \cos 0^{\circ})\\[ 5pt ] & = 68.6\ [\mathrm{N}]\end{align}\)

Load torque of motor shaft conversion

\(\begin{align}{T_L} & =\frac{{F} \cdot {P_B}}{2 \pi \cdot \eta} + \frac{ \mu_0 \cdot F_0 \cdot P_B}{2 \pi} \\[ 5pt ] & =\frac{68.6 \times 10 \times 10^{-3}}{2 \pi \times 0.9} + \frac{0.3 \times 22.9 \times 10 \times 10^{-3}}{2 \pi} \\[ 5pt ] & \fallingdotseq0.13\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

Here, the ball screw preload \(\displaystyle F_0 = \frac{1}{3} \ F \ \).

(5) Calculate the Load Inertia J_L [kg·m²]

Inertia of Ball Screw

\(\begin{align} {J_B} & = \frac{\pi}{32}\cdot \rho\cdot{L_B}\cdot{{D_B}^4}\\[ 5pt ] & = \frac{\pi}{32}\times\ 7.9 \times 10^3\ \times 1000 \times 10^{-3}\times {\left(25\times 10^{-3} \right)}^4\\[ 5pt ] & \fallingdotseq 3.03 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)

Inertia of Table and Load

\(\begin{align}{J_m} & = \mathrm{m}\ \left(\frac{P_B}{2\pi}\right)^2\\[ 5pt ] & = 100 \times \left(\frac{10 \times 10^{-3}}{2\pi}\right)^2\\[ 5pt ] & \fallingdotseq 2.53 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)

Load inertia

\(\begin{align}J_L &=J_B + J_m\\ &= 3.03 \times10^{-4} + 2.53 \times 10^{-4}\\ & = 5.56 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)

(6) Tentative Servo Motor Selection

Safety factor S_f = 1.5.

\(\begin{align}\text{Load torque}\ {T'}_L &=Sf \cdot T_L\\[ 5pt ] &=1.5 \times 0.13\\[ 5pt ] &= 0.195 [\mathrm{N}\cdot \mathrm{m}] \end{align}\)

\(\begin{align}\text{Load Inertia}\ J_L =5.56 \times 10^{-4} \ [\mathrm{kg}\cdot \mathrm{m}^2] \end{align}\)

Therefore, select the servo motor which has a speed of 1200 [r/min], outputs the rated torque 0.195 [N·m] or more and whose permissible load inertia is 5.56 × 10⁻⁴ [kg·m²] or more.

→ NXM620A+NXD20-A
Rated speed N = 3,000 [r/min]
Rated torque T_M = 0.637 [N·m]
Rotor inertia J₀ = 0.162 × 10⁻⁴ [kg·m²]
Permissible load inertia J = 8.1 × 10⁻⁴ [kg·m²]
Maximum instantaneous torque T_MAX = 1.91 [N·m]
The above values are appropriate.

(7) Calculate the Acceleration Torque T_a [N·m] and Deceleration Torque T_d [N·m]

Calculate the acceleration/deceleration torque using the formula below.

\(\begin{align}T_a (= T_d) & = \frac{(J_L + J_0) \ N_M }{9.55 \ t_1} \\[ 5pt ] & =\frac{(5.56 \times 10^{-4} + 0.162 \times 10^{-4})\times 1200}{9.55 \times 0.1} \\[ 5pt ] & \fallingdotseq \ 0.72\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)

(8) Calculate the Required Torque T [N·m]

\(\begin{align}T& = T_a + T_L \\[ 5pt ] & = 0.72 + 0.13\\[ 5pt] &= 0.85 \ [\mathrm{N}\cdot \mathrm{m}] \end{align}\)

The required torque is less than the maximum instantaneous torque of NXM620A+NXD20-A of 1.91 [N·m], so the NXM620A+NXD20-A can be used.

(9) Determine a Torque Pattern

Determine a torque pattern using operating cycle, acceleration/deceleration torque, load torque and acceleration time.

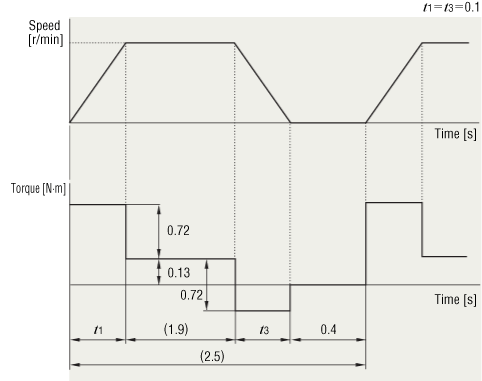
(10) Calculate the Effective Load Torque T_rms [N·m]

Calculate the effective load torque T_rms using the torque pattern and formula below.

\(\begin{align} T_{rms}& = \root \of {\frac{(T_a + T_L)^2 \cdot t_1 + {T_L}^2 \cdot t_2 + (T_d - T_L)^2 \cdot t_3}{t_f}} \\[ 5pt ] & = \root \of {\frac{(0.72 + 0.13)^2 \times 0.1 + {0.13}^2 \times 1.9 + (0.72 - 0.13 )^2 \times 0.1}{2.5} } \\[ 5pt ] & \fallingdotseq 0.24 \ [ \mathrm{N} \cdot \mathrm{m}] \end{align}\)

Here, t₁ + t₂ + t₃ = 2.1 [s] from the operating cycle and t₁ = t₃ = 0.1 for acceleration and deceleration time. Therefore, t₂ = 2.1 − 0.1 × 2 = 1.9 [s]
The ratio (effective load safety factor) of T_rms and the rated torque of servo motor T_M is expressed by the formula below.

\(\begin{align} \frac{T_M}{T_{rms}}& = \frac{0.637}{0.24} \\[ 5pt ] & = 2.65 \end{align}\)

Generally, a motor can operate at an effective load safety factor of 1.5∼2 or more.

NORTH AMERICA

EUROPE

ASIA

Selecting a Motor: Selection Example - Ball Screw Mechanism

For AC motors