Cooling Fan: Noise

What is Noise?

We generally refer to sounds that we find unpleasant as noise. In the case of a cooling fan, the rotation of the blades causes changes in air pressure, leading to the generation of noise. The greater the change in air pressure, the louder the noise becomes.

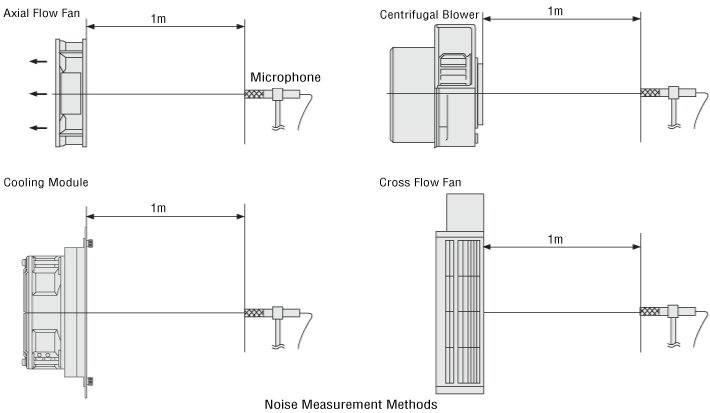
Noise Measurement

The noise level of Oriental Motor’s cooling fans is measured in the A-weighted sound pressure level at a distance of 1 m from the intake side (at a point above the center line of the intake side).

Noise Measurement Methods

Composition of Noise

This section explains the noise level when using 2 cooling fans, each of which produces 40 dB of noise.
Because the noise level is expressed in decibels, simple arithmetic sum does not apply. To represent this, it is necessary to first consider sound as energy, and then calculate the increase in sound pressure based on that.

The relationship between sound energy J and sound pressure P is expressed in the following formula: \(\displaystyle J = \frac{P^2}{\rho c}\) (ρ: air density, c: speed of sound propagation)

When using this relationship to express the noise level in decibels, it becomes as follows.

\(\begin{align} \text{Noise Level} & = 20\mathrm{log}\ P/P_0\\[ 3pt ] & = 10\mathrm{log}\ J/J_0 \end{align}\)
P
Actual sound pressure
J
Measured noise energy
P0, J0
The minimum noise energy discernible by humans

In other words, in this formula the noise level is expressed in decibels based on the reference energy of J0. Using this formula to calculate sound pressure, because there are n cooling fans, the energy of the sound becomes n times, and it can be determined as follows.

\(\begin{align} \text{Noise Level} & = 10\mathrm{log}\ \mathrm{n}\cdot J/J_0\\[ 3pt ] & = 10\mathrm{log}\ J/J_0 + 10\mathrm{log}\ \mathrm{n} \end{align}\)

This means that the increase in noise when n cooling fans are operated simultaneously is 10 log n [dB].
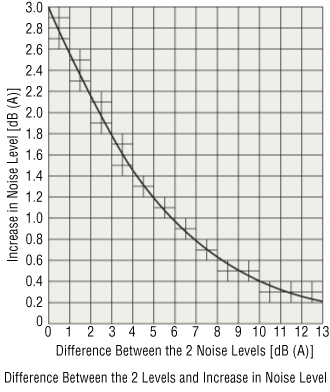
Here, because there are two cooling fans (n=2), the noise level increases by 10 log 2, which is 3 [dB]. Therefore, if two 40 dB cooling fans are operated simultaneously, the resulting noise level would be 43 dB.

Next, let's consider the noise level when a 40 dB cooling fan and a 50 dB cooling fan are operated simultaneously. Again, it is not possible to obtain the combined noise level by simple arithmetic sum.

Composition of Noise

If 40 dB of noise is combined with 50 dB, the resulting increase in noise level is only 0.4 dB. In other words, since the noise level is always governed by the higher value, it is important to reduce the noise of the cooling fan with the higher noise level when cooling fans with different noise levels are operated simultaneously.

Difference between the 2 Levels and Increase in Noise Level

Distance and Noise

Noise level decreases as the distance from the sound source increases.
The distance attenuation of this noise level can be expressed by the following formula.

\( \mathrm{SPL}_2 = \mathrm{SPL}_1 - 20 \mathrm{log}\ \mathrm{r_2}/\mathrm{r_1} \)
SPL2
Noise level at distance r2.
SPL1
Noise level at distance r1.

Let's calculate the noise level of a cooling fan measured at 2 m when the cooling fan is 1 m from the intake side and has a noise level of 40 dB.
Given that r2=2 m r1=1 m, and SPL1=40 dB, substituting these values, we get the following.

\( \begin{align}\mathrm{SPL}_2 & = 40- 20 \mathrm{log}\ 2/1\\[ 3pt ] & = 34\ [\mathrm{dB}]\end{align} \)

At a distance of 2 m, there is a decrease of 6 dB.
The value 20 log (r2/r1) represents the ratio of two distances, so if the values used above were 3 m and 6 m, the result would have been the same. From this, if the noise level at a certain distance is known, it becomes possible to estimate the noise level at a different distance.

Technical Reference