Selecting an Electric Linear Slide/Electric Cylinder: Calculation of Load Moment - Electric Linear Slides -

Selection Method

The Load Moment

When a load is transported by an electric linear slide, if the position of the center of gravity of the load is offset from the table center (fulcrum), a load moment will act on the linear guide.
The direction of action applies to 3 directions: pitching (MP), yawing (MY), and rolling (MR), depending on the position of the offset.

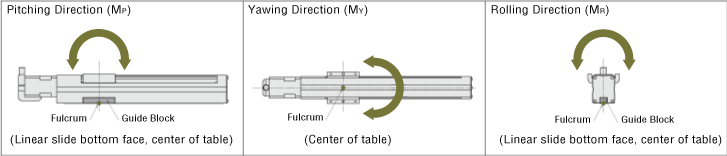
Linear Slide: Direction of action applies to 3 directions: pitching (MP), yawing (MY), and rolling (MR), depending on the offset position

Even though the selected electric linear slide satisfies the load mass and positioning time requirements, when the center of gravity of the load is overhung from the table's center of gravity (fulcrum), the operating lifetime may decrease due to the load moment. Load moment calculations must be completed and whether the conditions are within specification values must be checked. The moment applied under static conditions is the static permissible moment. The moment applied under movement is the dynamic permissible moment, and both must be checked.

Calculate the load moment applied to electric linear slide from the load and the direction the load is applied. Check that the static permissible moment and dynamic permissible moment are not exceeded, and check that strength is sufficient.

Calculate the load moment applied to linear slide from the load and the direction the load is applied. Check that the static permissible moment and dynamic permissible moment are not exceeded, and check that strength is sufficient
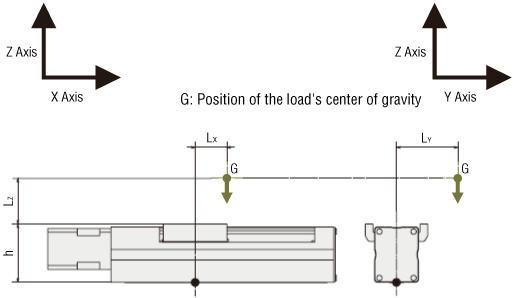
m
Load Mass (kg)
g
Gravitational Acceleration 9.807 (m/s2)
a
Acceleration (m/s2)
h
Electric Linear Slide Table Height (m)
LX
Overhang Distance in the X-Axis Direction (m)
LY
Overhang Distance in the Y-Axis Direction (m)
LZ
Overhang Distance in the Z-Axis Direction (m)
ΔMP
Load Moment in the Pitching Direction (N·m)
ΔMY
Load Moment in the Yawing Direction (N·m)
ΔMR
Load Moment in the Rolling Direction (N·m)
MP
Permissible Moment in the Pitching Direction (N·m)
MY
Permissible Moment in the Yawing Direction (N·m)
MR
Permissible Moment in Rolling Directions (N·m)
  • Load Moment Formula:
\(\begin{align}\frac{|\Delta \mathrm{M_P}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_Y}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_R}|}{\mathrm{M_R}} \leqq 1 \end{align}\)

When there are several overhung loads, etc., it is determined by the sum of moments from all loads.

  • For Multiple Loads (n pieces)
\(\begin{align}\frac{|\Delta \mathrm{M_{P1}} + \Delta \mathrm{M_{P2}} + \cdots \Delta \mathrm{M_{Pn}}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_{Y1}} + \Delta \mathrm{M_{Y2}} + \cdots \Delta \mathrm{M_{Yn}}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_{R1}} + \Delta \mathrm{M_{R2}} + \cdots \Delta \mathrm{M_{Rn}}|}{\mathrm{M_R}} \leqq 1 \end{align}\)

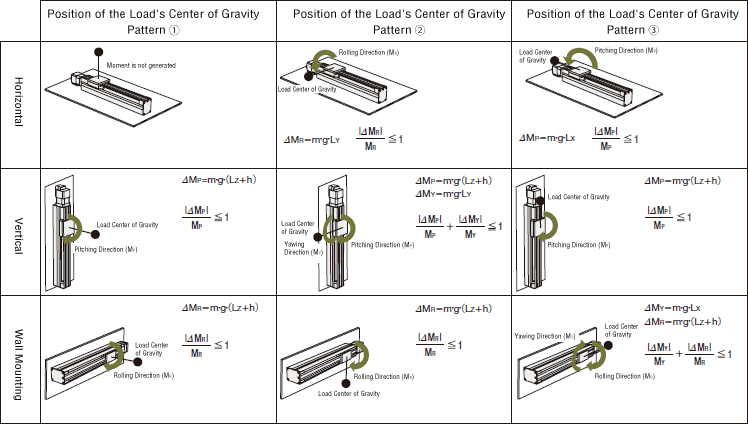
Concept of Load Moment Application

Concept of Static Moment Application

The following illustrations show typical examples of the combinations between how the Electric Linear Slide is installed and how overhung the load is. Select one of these examples that corresponds to your usage conditions. Calculate load moments (ΔMP, ΔMY, ΔMR) when the electric linear slide is at stop, and check if it is used within the range of static permissible moments (MP, MY, MR) using the formula to determine load moment.

Concept of Static Moment Application

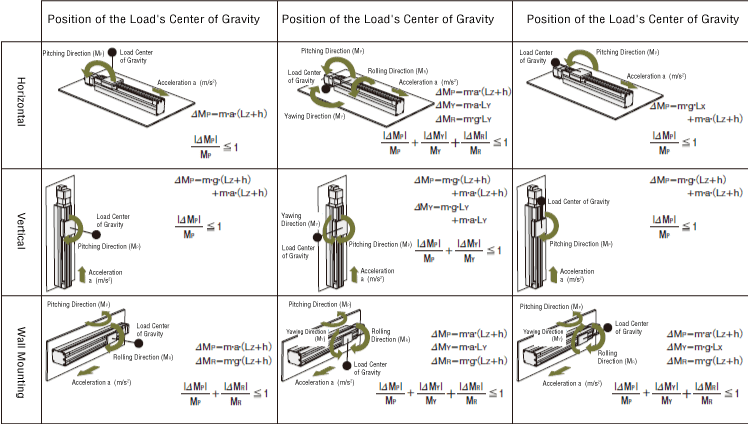
Concept of Dynamic Moment Application

The following illustrations show typical examples of the combinations between how the Electric Linear Slide is installed and how overhung the load is. Select one of these examples that corresponds to your usage conditions. Calculate load moments (ΔMP, ΔMY, ΔMR) when the electric linear slide is moving (taking into account acceleration), and check if it is used within the range of dynamic permissible moments (MP, MY, MR) using the formula to determine load moment.

Concept of Dynamic Moment Application

The expected life distance of the linear guides of the electric linear slides is designed with reference to the life of each series.
However, under conditions where the load moment formula is greater than 1, the expected life distance will be less than the expected value.
Use the formula below to approximate the expected life distance.

\(\begin{align} \text{Expected Life Distance}(\mathrm{km}) = 5000 \mathrm{km^\ast}\times \left( \frac{1}{ \frac{|\Delta \mathrm{M_P}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_Y}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_R}|}{\mathrm{M_R}}} \right)^3\end{align}\)
  • *The expected life varies depending on the product. Refer to here for details.

Selection Procedure and Calculation Formula